ভারতে গণিতচর্চাঃ পশ্চিমাদের আগে গণিতের এমন কিছু অভিনব উদ্ভাবন, যা ভারতীয়রা বিপ্লব ঘটিয়েছিল।গণিত হল এমন একটি বিষয় (বিজ্ঞান) যা আকার, পরিমাণ, গণনা এবং বিন্যাসের যুক্তি নিয়ে কাজ করে। গণিত আমাদের চারপাশে, আমরা যা কিছু করি।
মোবাইল ডিভাইস, স্থাপত্য (প্রাচীন ও আধুনিক), শিল্প, অর্থ, প্রকৌশল এবং এমনকি খেলাধুলাসহ আমাদের দৈনন্দিন জীবনের সবকিছুর জন্য এটি একটি নির্ধারিত স্থান। এটি মানুষের মন দ্বারা প্রাপ্ত বিমূর্ততার উচ্চ স্তরের প্রতিনিধিত্ব করে।
ভারতে গণিতের শিকড় বৈদিক সাহিত্যে রয়েছে যা প্রায় ৭০০০ বছর পুরনো। ১০০০ খ্রিস্টপূর্বাব্দ এবং ১০০০ খ্রিস্টাব্দের মধ্যে, গণিতের উপর বিভিন্ন ধারণা ভারতীয় গণিতবিদরা দিয়েছিলেন। এর মধ্যে প্রথমবারের মতো শূন্যের ধারণা, বীজগণিত এবং অ্যালগরিদমের কৌশল, বর্গমূল এবং ঘনক্ষেত্র অন্তর্ভুক্ত ছিল। প্রাচীন ভারতের গণিতের বিভিন্ন উদাহরণ রয়েছে যা আজও প্রযোজ্য।
গণিত কথাটির অর্থ হল গণনা সম্পর্কীয় শাস্ত্র। এটি বিজ্ঞানের অন্যতম প্রধান শাখা। গণিতের শুরু কবে ও কোথায় এ প্রশ্নের সঠিক উত্তর দেওয়া সম্ভব নয়। অনেকের মতে গণিতের আদিভূমি মিশর। যদিও এ নিয়ে বিতর্ক আছে। এর কারণ সেই সময় ব্যাবিলন এবং চীন এর পাশাপাশি আমাদের ভারতবর্ষেও উন্নতমানের গণিত চর্চা হত, যার স্বপক্ষে বহু প্রমাণ পাওয়া গেছে। তাই অনেক পণ্ডিতের মতে ভারতবর্ষই গণিতশাস্ত্রের উৎপত্তি স্থল। প্রশ্ন আসতে পারে এমন দাবি করার পিছনে যুক্তি কী?
সিন্ধু সভ্যতাকেই ধরে নেওয়া হয় ভারতের মাটিতে গণিতের পথচলার শুরুর সময়কাল। কারণ, এর আগের কোনো সভ্যতার নিদর্শন আজও আমরা খুঁজে পাইনি। সিন্ধু সভ্যতার ধ্বংসাবশেষ থেকে যে লিপির নিদর্শন পাওয়া গেছে তা আজও পাঠ ও মর্মোদ্ধার করা সম্ভব হয় নি। তাই সে যুগের গণিতচর্চার প্রকৃত স্বরূপ আজও আমাদের অজানা। তবে ধ্বংসাবশেষে ছড়িয়ে ছিটিয়ে থাকা বিভিন্ন নিদর্শন দেখে একথা অনুমান করতে অসুবিধা হয় না যে, এই উপত্যকাবাসীদের গণিতজ্ঞান যথেষ্ট উন্নতমানের ছিল। এই সভ্যতার উন্মেষ হয়েছিল ৩৫০০ – ৩৩০০ খ্রিষ্ট পূর্বাব্দের মধ্যে। সুতরাং ভারতীয় গণিতই প্রাচীনতম কিনা তা নিয়ে বিতর্ক থাকলেও মিশর, সুমেরীয় বা চীনের থেকে যে পিছিয়ে ছিল না এ কথা অনস্বীকার্য।
মূলত, ভারতবর্ষে গণিত এর চর্চা সেই বৈদিক যুগ থেকে হয়ে আসছে। বৈদিক মনীষীগণ দ্বারা গণিতের পরিপূর্ণ চর্চাই ভারতবর্ষের জ্যোতির্বিজ্ঞানকে উৎকর্ষের শিখরে উঠতে সাহায্য করেছিল বলে মনে করা হয়। বৈদিক যুগে গণিতের ভিত্তি বেদে বর্ণিত ১৬ টি সূত্র ও ১৩ টি উপসূত্রে অন্তর্নিহিত ছিল। বৈদিকযুগে মূলতঃ দশমিক পদ্ধতিতেই গণনাকার্য সম্পন্ন হত। যজুর্বেদ সংহিতায় প্রাপ্ত বিভিন্ন সংখ্যা যেমন; অর্বুদ(১০০০০০০০), নর্বুদ(১০০০০০০০০), সমুদ্র(১০০০০০০০০০), পরার্ধ(১০০০০০০০০০০০০) থেকে জানা যায় যে বিশালায়তন সংখ্যার ধারণাও হিন্দু গণিতজ্ঞদের কল্পনাতীত ছিল না।
সমসাময়িক কোনও জাতি সম্ভবত এত বৃহৎ সংখ্যা কল্পনা করতে সক্ষম ছিল না। নিম্নে বর্ণিত সংখ্যাপ্রবাহ দুটিকে লক্ষ্য করা যাকঃ ১,৩,৫,…,৯৯ ২৪,৪৮,৯৬,১৯২,………,৩৯৩২১৬ প্রথমটির নাম সমান্তর প্রগতি এবং দ্বিতীয়টির নাম গুণোত্তর প্রগতি। ‘তৈত্তিরীয় সংহিতা’ ও ‘পঞ্চবিংশ ব্রাহ্মণ’ এ যথাক্রমে উপরোক্ত প্রগতিগুলির উল্লেখ পাওয়া যায়।
এত গেলো পাটিগণিতের কথা। ‘শতপথ ব্রাহ্মণ’ এ হিন্দুদের জ্যামিতিক জ্ঞানেরও পরিচয় পাওয়া যায়। আমরা অনেকেই জানি, বৈদিক যজ্ঞানুষ্ঠানে একটি অন্যতম উপকরণ ছিল ‘মহাবেদী’; যার আকৃতি হল সমদ্বিবাহু ট্রাপিজিয়াম। এই সমদ্বিবাহু ট্রাপিজিয়াম এর ক্ষেত্রফল এবং বাহু-উচ্চতার বিভিন্ন সম্পর্ক হিন্দুরা জানতেন। ঋণাত্মক রাশি সম্পর্কেও তারা অবগত ছিলেন। সংস্কৃত ভাষায় আরেকটি অন্যতম সূত্র হল “শুলভা সূত্র”। শুলভা শব্দের অর্থ দড়ি বা ঐ ধরনের কিছু।
এই শুলভা সূত্র ব্যবহার করা হত হিন্দুদের মৃত্যুর পর বেদী তৈরীর কাজে। এটি এক ধরনের বৈদিক জ্ঞান, যেখানে বিভিন্ন ধরনের আগুনে পোড়ানোর বেদীর বিভিন্ন অর্থ তুলে ধরা হয়েছিল। উদাহরণ স্বরুপ বলা যায়, যারা স্বর্গে যেতে ইচ্ছুক, শুলভা সূত্র অনুযায়ী তাদের আগুনে পোড়ানোর বেদী হবে বকের আকৃতির। যারা ব্রাক্ষনদের মত পৃথিবী জয় করতে চায়, তাদের বেদী হত কচ্ছপ আকৃতির। এছাড়া রম্বস আকৃতির হবে তাদের বেদী, যারা অজাতশত্রু হতে চায়! বেদ থেকে প্রাপ্ত বেশ কিছু গুরুত্বপূর্ণ সূত্রগুলো হল:
অপাস্তমব্য
বৌধয়ন
মানব
ক্যাত্যায়ন
মৈত্রয়নী (মানব এর সাথে সাদৃশ্যপূর্ণ)
বরাহ
বধূলা
হিরন্যকেশ (অপাস্তমব্য এর সাথে সাদৃশ্য পূর্ণ)
এই সূত্রগুলোর বেশির ভাগই আবিষ্কৃত হয় ৮০০ থেকে ২০০ খ্রীষ্টপূর্বে। যাদের মধ্যে সবচাইতে প্রাচীন সূত্র হল বৌধয়ন। মজার ব্যাপার, অপাস্তমব্য ও বৌধয়নের সাথে পীথাগোরাসের সূত্র ও পীথাগোরিয়ান এরীয়র সাদৃশ্য লক্ষ্য করা গেছে। বিভিন্ন জ্যামিতিক আকৃতি, যেমন চতুর্ভূজ ও বর্গের অস্তিত্ব লক্ষ্য করা গেছে বৌধয়নের ভেতর। এছাড়া আছে, একটি সুনির্দিষ্ট জ্যামিতিক ক্ষেত্রের ক্ষেত্রফলকে অন্য একটি জ্যামিতিক ক্ষেত্রের ক্ষেত্রফলে রূপান্তর করার পদ্ধতি। আরো একটি বিস্ময়কর ব্যাপার হল, এই সূত্রের ভিতর √2 এর মান অত্যন্ত নির্ভুলভাবে বের করার উপায়ও বলা হয়েছে। যা আমরা পানিনি দ্বারা বর্ণিত ইতিহাস থেকে জানতে পারি।
এরপর প্রায় ১০০০ বৎসর গণিতের মৌলিক গবেষণার ক্ষেত্রে হিন্দুদের বিশেষ একটা অবদান লক্ষ্য করা যায় না। পরবর্তীতে আর্যভট্ট্(৪৭৬-৫৩০), ব্রহ্মগুপ্ত(৫৮৮-৬৬০ খ্রিঃ), বরাহমিহির(ষষ্ঠ শতাব্দীর প্রথম ভাগে ), গলস্ন (ষষ্ঠ শতাব্দীর প্রথম ভাগে), ভাস্কর(ষষ্ঠ শতাব্দীর শেষ ভাগে), মহাবীরাচার্য (নবম শতাব্দী ), শ্রীধর আচার্য (একাদশ শতাব্দীর প্রথম ভাগ), শ্রীপতি (একাদশ শতাব্দী), ভাস্করাচার্য (দ্বাদশ শতাব্দী) প্রমুখ মনীষীবৃন্দের কর্মালোকে হিন্দু গণিতশাস্ত্র আবার বিশ্বসভায় নিজের স্থান সুদৃঢ় করে তোলে।
গণিতশাস্ত্রে হিন্দু মনীষীদের সর্বাপেক্ষা উল্লেখযোগ্য অবদান হল দশমিক স্থানিক অঙ্কপাতন পদ্ধতি ও ‘শূন্য’ এর আবিষ্কার। অবশ্য এর আগে খ্রীষ্টপূর্ব ২০০ তে পিঙ্গলের ‘ছন্দসূত্রে’ শূন্যের ব্যবহার লক্ষ্য করা যায়। আর্যভট্ট রচিত ‘আর্যভটীয়’ নামক গ্রন্থে দ্বিঘাত প্রথম মাত্রার অনির্ণেয় সমীকরণের সমাধান ও π এর নির্ভুল মান এর উল্লেখ পাওয়া যায়।
বর্গমূল নির্ণয়ের পদ্ধতিও আর্যভট্টের আবিষ্কার। এসময়ের আরেকজন উল্লেখযোগ্য ব্যক্তি হলেন ব্রহ্মগুপ্ত। তিনি পিরামিড ফ্রাস্টাম এর আয়তন নির্নয় সম্পর্কিত সূত্র আবিষ্কার করেন। যাঁর কথা না বললে এই লেখা অপূর্ণ থেকে যাবে তিনি হলেন ভাষ্কর।
তাঁর লেখা বিখ্যাত গ্রন্থখানি হল চারখন্ডে সমাপ্ত ‘সিদ্ধান্ত শিরোমণি’। যার প্রথম ২টি খন্ড লীলাবতি ও বীজগণিত এ পাটীগণিত ও বীজগণিত এর বিভিন্ন বিষয় আলোচিত হয়েছে। “একটি ঋণাত্মক রাশিকে অপর একটি ঋণাত্মক রাশি দ্বারা গুণ করলে ধনাত্মক রাশি এবং একটি ঋণাত্মক ও অপর একটি ধনাত্মক রাশি গুণ করলে ঋণাত্মক রাশি পাওয়া যায়”, বীজগনিতের এই সিদ্ধান্ত ভাষ্কর এর আবিষ্কার। গণিত এর ছাত্র মানেই, “x=(-b±√(b^2-4ac))/2a” সূত্র সম্পর্কে অবগত। যার আবিষ্কারকের নাম শ্রীধর।
দ্বিঘাত সমীকরণের মাত্রা নির্ণয়ের এই সূত্রটি ‘শ্রীধরাচার্যের উপপাদ্য’ নামে প্রচলিত। এতো গেল পাটীগণিত ও জ্যামিতির কথা। এরপর ত্রিকোণমিতি। ত্রিকোণমিতিতেও হিন্দুদের সাফল্য অনস্বীকার্য। বরাহমিহির ‘পঞ্চসিদ্ধান্তিকা’ গ্রন্থে Sin 30 ও Sin 60 এর মান নির্ণয় করে দেখিয়েছেন। বর্তমান ত্রিকোণমিতিতে ব্যবহৃত মূল সূত্রগুলিও বরাহমিহির এর আবিষ্কৃত।
—————————————————————————-
যদি মাধ্যমিক পর্যায়ের গাণিতিক জ্ঞান সম্পন্ন কাউকে জিজ্ঞাসা করা হয় যে, “সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।” এটি কার উপপাদ্য, তবে সকলেই একবাক্যে বলবে, এটি “পিথাগোরাসের উপপাদ্য”। এই বিষয়ে কোনো সন্দেহ নেই যে এই উপপাদ্যটি সারা বিশ্বে পিথাগোরাসের উপপাদ্য হিসেবেই স্বীকৃত।
পিথাগোরাস খ্রিষ্টপূর্ব ৫৭২ অব্দের দিকে প্রাচীন গ্রিসে জন্মগ্রহণ করেন। তৎকালীন সময়ে গ্রিস ছিলো দর্শন চর্চা ও বৈজ্ঞানিক বীজ রোপনের প্রাণকেন্দ্র। তবে আমরা এটি জানি না যে তারও পূর্ববর্তী সময় হতেই আমাদের এই ভারতবর্ষেও একটি উৎকৃষ্ট সভ্যতা বিদ্যমান ছিলো, যেখানে ইতোমধ্যে দর্শন ও বিজ্ঞান, উভয়ই উৎকর্ষতা লাভ করেছিলো। “পিথাগোরাসের উপপাদ্য” নামক এই জ্যামিতিক ‘সম্পর্কটি’র স্পষ্ট উল্লেখ ও ব্যবহারের কথা পাওয়া প্রাচীন ভারতীয় কয়েকটি শুল্বসূত্র থেকে৷
“শুল্বসূত্র” নামটি অনেকের কাছেই নতুন লাগছে হয়ত। প্রথমে এটির পরিচয় দেওয়া যাক। বেদকে সঠিক ভাবে জানতে, বুঝতে ও তদানুসারে ক্রিয়াকর্ম করতে ছয় প্রকারের শাস্ত্র প্রয়োজন হয়। এগুলোকে একত্রে ষড় বেদাঙ্গ বলে। এই বেদাঙ্গের মধ্যে অন্যতম হলো “কল্প”। কল্প আবার চার ভাগে বিভক্ত।
- শ্রৌতসূত্র– বিভিন্ন যজ্ঞের বর্ণনা ও নিয়ম।
- গৃহ্যসূত্র– গৃহ কর্ম ও সংস্কারাদির নিয়ম।
iii. ধর্মসূত্র– বিভিন্ন বিধি-বিধান ও নিয়ম-নীতি।
- শুল্বসূত্র– যজ্ঞ বেদীর পরিমাপের পদ্ধতির বর্ণনা।
এই শুল্বসূত্র গুলোতে মূলত শ্রৌতযজ্ঞে ব্যবহৃত বিভিন্ন যজ্ঞবেদীর পরিমাপ পদ্ধতি বর্ণিত হয়েছে। প্রাচীনকালে এসব শুল্বসূত্রের পরিমাপ পদ্ধতি অনুসরণ করে যজ্ঞের বেদী নির্মাণ করা হতো। এসব শুল্বসূত্রের মধ্যে আজ কথা বলবো ৩টি নিয়ে। এগুলো হলো- ” কাত্যায়ন শুল্বসূত্র, বৌধায়ন শুল্বসূত্র এবং আপস্তম্ব শুল্বসূত্র”। গবেষকদের মতে, এই তিনটিসহ সকল শুল্বসূত্রের রচনাকাল পিথাগোরাসের পূর্ববর্তী। কিন্তু আশ্চর্যের বিষয় হচ্ছে, পিথাগোরাসের উপপাদ্যের ‘মূল সম্পর্ক’টি এই গ্রন্থগুলোতে বর্ণিত রয়েছে এবং প্রাচীন কালে এই সম্পর্ক অনুসরণ করে ভারতবর্ষে যজ্ঞবেদি তৈরি করা হতো।
“দীর্ঘচতুরস্রস্যাক্ষ্ণয়া রজ্জুস্তির্যঙ্মানী পার্শ্চমানী চ যৎ পৃথগ্ভূতে কুরুতঃ, তদুভয়ং করোতীতি ক্ষেত্রজ্ঞানম্।।”
[বৌধায়ন শুল্ব- ১।৪৮, কাত্যায়ন শুল্ব- ২।১১, আপস্তম্ব শুল্ব- ১।৭]
অর্থাৎ কোনো আয়তের কর্ণ বরাবর রশি টেনে তার বর্গ করা যায়, তবে সেই বর্গের ক্ষেত্রফল অপর দুই বাহু বরাবর রশির বর্গের যোগফলের সমান হবে।
এখানে স্পষ্টভাবে বোঝা যাচ্ছে, এটি মূলত পিথাগোরাসের উপপাদ্যের মূল সম্পর্ককে নির্দেশ করছে। পিথাগোরাস সমকোণী ত্রিভুজ দিয়ে সম্পর্কটি প্রকাশ করলেও এসব শুল্বসূত্রে আয়ত দিয়ে সম্পর্কটি বিবৃত হয়েছে।
এবার আসা যাক অপেক্ষাকৃত আধুনিক কালের ভারতীয় গণিতজ্ঞের দিকে। আর্যভট্ট (জন্ম- ৪৭৬ খ্রি) প্রাচীন ভারতের বিখ্যাত গণিতবিদ। কয়েকটি ভাগে বিভক্ত “আর্যভট্টীয়” তাঁর বিখ্যাত গ্রন্থ। এই গ্রন্থে [গণিতপাদ- ১৭] তিনি লিখেছেন,
“যশ্চৈব ভুজাবর্গঃ কোটীবর্গশ্চ কর্ণবর্গঃ সঃ।”
অর্থাৎ সমকোণী ত্রিভুজের ভুজের (আনুভূমিক বাহু) বর্গ এবং কোটির (উলম্ব বাহু) বর্গের সমষ্টি এর কর্ণের বর্গের সমান।
অর্থাৎ এসব প্রাচীন ভারতীয় গ্রন্থ হতে একটা ধারণা পাওয়া যায় যে, আমাদের প্রাচীন ভারতবর্ষ শিক্ষা, জ্ঞান, বিজ্ঞান, দর্শনে কতটা অগ্রগামী ছিলো।
এখানে উল্লেখ্য যে, এই পোস্টের মূল উদ্দেশ্য আমাদের প্রাচীন ভারতের বিস্মৃত তথ্য ও জ্ঞান ভাণ্ডার তুলে ধরা। এখানে আমি অন্য গোষ্ঠীর মতো দাবী করবো না যে, পিথাগোরাস কাত্যায়ন বা বৌধায়ন শুল্বসূত্র পড়েই তাঁর এই উপপাদ্য প্রদান করেছেন বা বেদ হতে নকল করে এই উপপাদ্য দিয়েছেন। কারণ এরকম দাবী নিতান্তই হাস্যকর ও অমূলক। কিন্তু এটা সত্য যে এই সম্পর্কটি প্রাচীন ভারত পিথাগোরাসের পূর্ব থেকেই জানতো।
হাজার হাজার বছর আগে যখন পৃথিবীতে জ্ঞান ও ধর্মকে একত্রিত করা হয়েছিল ঈশ্বরের উপাসনার জন্য, ঠিক তখন থেকেই আমাদের ভারত উপমহাদেশেও জ্যামিতি, গণিত ও ধর্মের বিভিন্ন রীতির সংমিশ্রন ঘটেছিল। সেই সময় হিন্দুধর্ম তথা সনাতন ধর্ম এতটাই সমৃদ্ধশালী ছিল যে, যা ভাষায় প্রকাশ করা সম্ভব নয়।
গণিতের উপর বিভিন্ন ধারণা ভারতীয় গণিতবিদরা দিয়েছিলেন। এর মধ্যে প্রথমবারের মতো শূন্যের ধারণা, বীজগণিত এবং অ্যালগরিদমের কৌশল, বর্গমূল এবং ঘনক্ষেত্র অন্তর্ভুক্ত ছিল। প্রাচীন ভারতের গণিতের বিভিন্ন উদাহরণ রয়েছে যা আজও প্রযোজ্য।
শূন্য আবিষ্কার
ভারতীয় গণিতবিদ-জ্যোতির্বিজ্ঞানী আর্যভট্ট না থাকলে সংখ্যাটি শূন্য হত না। যদিও মানুষ সবসময় কিছু না হওয়া বা কিছুই না হওয়ার ধারণা বুঝতে পারত। একটি অপেক্ষাকৃত নতুন ধারণা, এটি ভারতে সম্পূর্ণরূপে বিকশিত হয়েছিল। তার আগে, গণিতবিদরা সহজতম গাণিতিক গণনা করতে সংগ্রাম করেছিলেন। আজ, শূন্য – একটি প্রতীক (বা সংখ্যা) এবং একটি ধারণা মানে কোন পরিমাণের অনুপস্থিতি। জিরো আমাদের নেভিগেট করতে, জটিল সমীকরণ সম্পাদন করতে এবং কম্পিউটার কাজ করে দিয়েছে।
জিরোগ্রিন ইন্ডিয়া ফাউন্ডেশন বা জিরো প্রজেক্টের সেক্রেটারি পিটার গব্বেটস বলেন, “শূন্যকে ব্যাপকভাবে মানব ইতিহাসের অন্যতম সেরা উদ্ভাবন হিসেবে দেখা হয়, আধুনিক গণিত ও পদার্থবিজ্ঞানের ভিত্তি।
বীজগণিত
প্রাচীন কালে বীজগণিতের ক্ষেত্রে ভারতের বড় অবদান ছিল। প্রাচীন ভারতে, গণিত নামক ঐতিহ্যগত বীজগণিতের বিকাশের আগে জানা ছিল। এটি বীজগণিত নাম থেকে উদ্ভূত, যা গণনার বীজগণিতিক রূপকে দেওয়া হয়েছিল। বীজগণিতম মানে ‘অন্যান্য গণিত’ (বিজ মানে দ্বিতীয় এবং গণিত মানে গণিত)।
৫ম শতাব্দীর কাছাকাছি ভারতে, গণিতের একটি পদ্ধতি যা জ্যোতির্বিজ্ঞান গণনাকে সহজতর করে। সেই সময়ে এর প্রয়োগ ছিল জ্যোতির্বিজ্ঞানে সীমাবদ্ধ কারণ এর অগ্রদূতরা ছিলেন জ্যোতির্বিজ্ঞানী। যেহেতু জ্যোতির্বিজ্ঞান গণনা জটিল এবং অনেক ভেরিয়েবল জড়িত যা অজানা পরিমাণের উদ্ভবের মধ্যে যায়। বীজগণিত গণনার একটি পদ্ধতি এবং এই বৈশিষ্ট্য দ্বারা, এটি গতানুগতিক গাণিতিকের চেয়ে বেশি সহজ করে।
ত্রিকোণমিতি
ত্রিকোণমিতির উৎপত্তি প্রাচীন ভারতে। ভারত থেকে মধ্যপ্রাচ্যে ভ্রমণ এবং সর্বত্র মানুষ এটি গ্রহণ করেছিল। এখান থেকে এটি আরবদের মধ্য দিয়ে ইউরোপে গিয়েছিল এবং অনেক পরিবর্তনের মধ্য দিয়ে তার বর্তমান রূপে পৌঁছেছিল। প্রাচীনকালে, ত্রিকোণমিতি জ্যোতির্বিজ্ঞানের একটি অংশ হিসাবে বিবেচিত হত।
সূর্য অনুষ্ঠানের সূচনায় অবদানের জন্য আমরা সিদ্ধান্তকে (সংস্কৃত জ্যোতির্বিজ্ঞান রচনা) সম্মান করি। ঐতিহাসিকরা আর্যভট্ট, ব্রহ্মগুপ্ত, ভাস্কর -১ এবং ভাস্কর -২ কে ত্রিকোণমিতির প্রধান প্রতিপাদক বলে মনে করেন। ভাস্কর- I ৯০ এর বেশি কোণের জন্য সাইন ফাংশনের মান খুঁজে বের করার জন্য সূত্র দিয়েছে অন্যদিকে, ভাস্কর -2, ১৮০, ৩৬০, ৫৪০এবং ৭২০ এর মতো তীব্র কোণের ত্রিকোণমিতিক অনুপাত গণনার জন্য সঠিক অভিব্যক্তি দিয়েছে।
দশমিক পদ্ধতি এবং চতুর্ভুজ সূত্র
ভারতীয় গণিতের শাস্ত্রীয় যুগে (400 খ্রিস্টাব্দ পূর্ব থেকে 1600 খ্রিস্টাব্দ ), আর্যভট্ট, ব্রহ্মগুপ্ত, মহাবীর, ভাস্কর দ্বিতীয়, সঙ্গমগ্রামের মাধব এবং নীলকণ্ঠ সোমায়াজীর মতো পণ্ডিতগণ উল্লেখযোগ্য অবদান রেখেছিলেন। আজ সারা বিশ্বে ব্যবহৃত দশমিক সংখ্যা পদ্ধতি ভারতীয় গণিতে প্রথম রেকর্ড করা হয়েছিল।
এটি খ্রিস্টীয় সপ্তম শতাব্দীতে যখন ব্রহ্মগুপ্ত চতুর্ভুজ সমীকরণ সমাধানের প্রথম সাধারণ সূত্র খুঁজে পান। দশমিক পদ্ধতি (বা হিন্দু সংখ্যা পদ্ধতি), যা আরবি সংখ্যাসূচক ব্যবস্থার পূর্বসূরী ছিল, ভারতে খ্রিস্টীয় প্রথম এবং ষষ্ঠ শতাব্দীর মধ্যে বিকশিত হয়েছিল।
ফিবোনাকি নম্বর
ফিবোনাকি সিকোয়েন্স হল সংখ্যার একটি সিরিজ যেখানে একটি সংখ্যা তার আগে দুটি সংখ্যা যোগ করে পাওয়া যায়। 0 এবং 1 থেকে শুরু করে এই ক্রমটি 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 এবং এভাবে চলে। এটি প্রথম বীরহঙ্কা, গোপাল এবং হেমচন্দ্র কর্তৃক পিঙ্গলার আগের লেখার হিসেবে বর্ণনা করা হয়েছিল।
দৈর্ঘ্য
খ্রিস্টপূর্ব 1500 এর আগে সিন্ধু সভ্যতা স্কেল ব্যবহার করা হয়েছিল । হাতির দাঁতের তৈরি খননকালে পাওয়া, শাসকরা এটিতে দশমিক উপবিভাগের আশ্চর্যজনক নির্ভুলতা প্রকাশ করেছিলেন।
সিন্ধু সভ্যতার লোকেরা দৈর্ঘ্য, ভর এবং সময় পরিমাপে দারুণ নির্ভুলতা অর্জন করেছিল। রাখান সমান ওজন এবং পরিমাপের একটি সিস্টেম বিকাশকারী প্রথম ব্যক্তিদের মধ্যে ছিলেন। সিন্ধু সভ্যতা খনন থেকে পাওয়া জিনিস সিন্ধু অঞ্চলে বড় আকারের পরিমাপ পদ্ধিতির নির্দেশ করে। তাদের ক্ষুদ্রতম বিভাগ, গুজরাটের লোথালে পাওয়া একটি হাতির দাঁতের স্কেলে উৎকীর্ণ ছিল, প্রায় 1.704 মিমি, ব্রোঞ্জ যুগের স্কেলে রেকর্ড করা সবচেয়ে ছোট বিভাগ।
ওজন পরিমাপ
ভারতে পরিমাপ ব্যবস্থার ইতিহাস সিন্ধু সভ্যতার প্রথম দিকে শুরু হয়, খ্রিস্টপূর্ব ৫ম সহস্রাব্দের জীবিত নমুনার সাথে। প্রারম্ভিক সময় থেকেই মানসম্মত ওজন এবং পরিমাপ গ্রহণ দেশের স্থাপত্য, লোক ও ধাতুর নিদর্শন দেখায়। মৌর্য সাম্রাজ্য (খ্রিস্টপূর্বাব্দ) দ্বারা ওজন ও পরিমাপের একটি জটিল ব্যবস্থা গ্রহণ করা হয়েছিল, যা এই ব্যবস্থার ব্যবহারের নিয়মও নির্ধারণ করেছিল। পরবর্তীতে, মুঘল সাম্রাজ্য মুঘল ভূমি সংস্কারের অংশ হিসাবে ভূমি মালিকানা নির্ধারণ এবং ভূমি কর আদায়ের জন্য মানসম্মত ব্যবস্থা ব্যবহার করে।
মোট 558 টি ওজন যন্ত্র মহেঞ্জোদারো, হরপ্পা এবং চানহু-দারো থেকে খনন করার সময় পাওয়া গিয়েছিল, তারা পাঁচটি ভিন্ন স্তর থেকে খনন করা ওজনের যন্ত্র মধ্যে পরিসংখ্যানগতভাবে উল্লেখযোগ্য পার্থক্য খুঁজে পায়নি। প্রত্যেকটির গভীরতা ছিল প্রায় 1.5 মিটার। 13.7-জি ওজন সিন্ধু উপত্যকায় ব্যবহৃত এককগুলির মধ্যে একটি। স্বরলিপি বাইনারি এবং দশমিক পদ্ধতির উপর ভিত্তি করে ছিল।
ভারতীয় গণিতবিদের জ্যামিতি ক্ষেত্রে অবদান
ভারতীয় গণিতবিদরাও জ্যামিতির ক্ষেত্রে অবদান রেখেছেন। রেখা গণিতা (লাইন কাউন্টিং) নামে গাণিতিক অ্যাপ্লিকেশনের একটি পদ্ধতি ছিল। সুলভা সূত্র, যার আক্ষরিক অর্থ ‘আইনের শাসন’, বেদী ও মন্দির নির্মাণের জ্যামিতিক পদ্ধতি প্রদান করে। মন্দিরগুলির বিন্যাসকে বলা হত মণ্ডল। এই অঞ্চলের কিছু গুরুত্বপূর্ণ কাজ অপস্তম্ব, বৌধায়ন, হিরণ্যকেশীন, বরাহ এবং ভাদুলা দ্বারা সম্পন্ন হয়েছে।
অসীম সিরিজ
কেরালার গণিতবিদরা মধ্যবর্তী সাইন মান গণনা করার জন্য দ্বিতীয় অর্ডার প্রবর্তনের জন্য নিয়ম প্রণয়ন করেছিলেন। কেরলের গণিতবিদ মাধব নিউটনের প্রায় তিনশ বছর আগে সাইন এবং কোসাইন সিরিজ আবিষ্কার করেছিলেন। এই অর্থে, আমরা মাধবকে গাণিতিক বিশ্লেষণের প্রতিষ্ঠাতা হিসাবে বিবেচনা করতে পারি। মাধব (আনুমানিক 1340-1425 খ্রিস্টাব্দ) প্রাচীন ভারতীয় গণিতের সীমাবদ্ধ প্রক্রিয়া থেকে অনন্ত পর্যন্ত তার সীমানা-রূপান্তরের চিকিত্সার জন্য প্রথম সিদ্ধান্ত গ্রহণকারী পদক্ষেপ গ্রহণ করেছিলেন। তার অবদানের মধ্যে রয়েছে বৃত্তাকার এবং ত্রিকোণমিতিক ফাংশনের অসীম-সিরিজ সম্প্রসারণ এবং সীমাবদ্ধ সিরিজের আনুমানিকতা। পাই এবং সাইন এবং কোসাইন কাজের জন্য তার পাওয়ার সিরিজটি পরবর্তী লেখকদের দ্বারা শ্রদ্ধার সাথে উল্লেখ করা হয়েছে।
বাইনারি কোড
বাইনারি সংখ্যা কম্পিউটার পরিচালনার ভিত্তি। 1695 সালে জার্মান গণিতবিদ গটফ্রাইড লিবনিজ পশ্চিমের মধ্যে বাইনারি সংখ্যা আবিষ্কার করেছিলেন। যাইহোক, নতুন প্রমাণ করে যে বাইনারি সংখ্যা ভারতে ২য় শতাব্দীর আগে ব্যবহার করা হয়েছিল, যা পশ্চিমের আবিষ্কারের 1500 বছরেরও বেশি আগে।
এই আবিষ্কারের উৎস হল পিংগালের একটি বাদ্যযন্ত্র যার নাম “ছন্দশাস্ত্র” যার অর্থ মিটারের বিজ্ঞান। এই পাঠ্যটি “সূত্র” বা কামোত্তেজক বিবৃতিতে পড়ে। এটি সংক্ষিপ্ত কিন্তু গভীর বিবৃতির বিস্তারিত আলোচনা পরবর্তী মন্তব্যগুলিতে পাওয়া যায়। দ্বিতীয় শতকে “ছন্দশাস্ত্র” এর যাত্রা শুরু হয়।

পাই
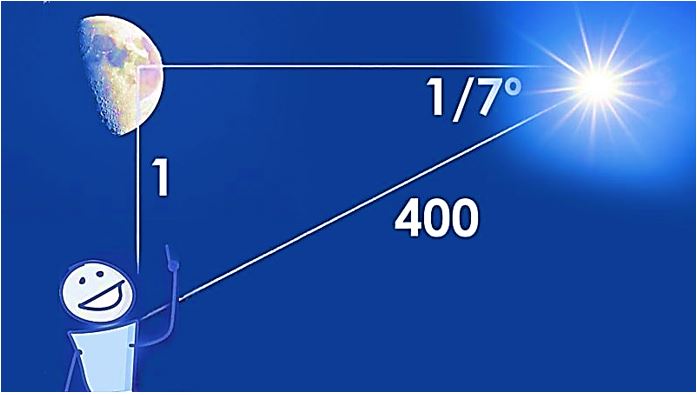
ভারতীয় গণিতজ্ঞরা গণিতের সবচেয়ে গুরুত্বপূর্ণ সংখ্যা ‘পাই’ এর রহস্যের সমাধান করেছে। ‘পাই’ হল একটি বৃত্তের পরিধি ও ব্যাসের অনুপাতের সংখ্যাগত মান। এটি এমন একটি সংখ্যা যেটা সব ধরণের গণনায় ব্যবহার হয়। তবে এর সবচেয়ে বেশি ব্যবহার হয় প্রকৌশল এবং স্থাপত্যবিদ্যায়।
কেননা, যেকোনো বক্ররেখা পরিমাপের জন্য ‘পাই’ এর প্রয়োজন। শত শত বছর ধরে, গণিতজ্ঞরা পাই-এর সুনির্দিষ্ট মান বের করার চেষ্টা করেছেন।
পরে ষষ্ঠ শতকে ভারতীয় গণিতবিদ আর্যভট্ট এ নিয়ে একটি সুনির্দিষ্ট ধারণা দেন। আর সেটা হল ৩.১৪১৬। পৃথিবীর পরিধি পরিমাপের জন্য তিনি এই সংখ্যা ব্যবহার করেছিলেন। তার গণনা অনুযায়ী পৃথিবীর পরিধি ৩৯,৯৬৮ কিলোমিটার। যেটা কিনা সর্বশেষ পরিমাপের (৪০,০৭৫ কিলোমিটার) সবচেয়ে কাছাকাছি মান।
ছবির উৎস,GETTY IMAGES
তিনি বুঝতে পেরেছিলেন যে বিভিন্ন ভগ্নাংশ যোগ এবং বিয়োগ করে পাই এর জন্য সঠিক সূত্র নির্ধারণ করা সম্ভব।
এই সূত্রটি এখনও বিশ্বজুড়ে অনেক বিশ্ববিদ্যালয়ে পড়ানো হয়। তবে শেখানে শেখানো হয় যে এটি ১৭ শতকের জার্মানির গটফ্রাইড উইলহেম লিবনিজ আবিষ্কার করেছেন।ভারতে গণিতচর্চা
ভাবতেই অবাক লাগে যে সময় পৃথিবীর অধিকাংশে মানবসভ্যতার ছোঁয়া পর্যন্ত লাগেনি তখন ভারতবর্ষের বিভিন্ন আশ্রমে ঋষিগণ নিমগ্ন ছিলেন বিজ্ঞানের মহাযজ্ঞে। এর কারণ বৈদিক যুগে এদেশের সমাজ ব্যবস্থা মূলত ধর্মের উপর প্রতিষ্ঠিত ছিল। ধর্ম কর্মের জন্য প্রয়োজন হত নানা ধরণের যজ্ঞাদি ক্রিয়া কান্ড। এই যজ্ঞানুষ্ঠানের একটি অপরিহার্য অঙ্গ ছিল যজ্ঞবেদী নির্মাণ। যার জন্যই সংখ্যা ও জ্যামিতির বিভিন্ন বিস্ময়কর বৈশিষ্ট্যই গণিতবিদ ও পুরোহিতদের অনুপ্রাণিত করেছিল গণিতশাস্ত্রকে বিভিন্ন ধর্মবিষয়ক কাজে ব্যবহার করার। আর সেই থেকেই শুরু হয় ভারতবর্ষে হিন্দুদের গণিতচর্চা।
আর পড়ুন……..